When it comes to the realm of Logic Problem Solving, grappling with complex scenarios and puzzling challenges is made more manageable with the aid of programming assignment help, offering learners a structured approach to develop and implement logical solutions with precision.
Question 1 (1st of 3)
a)An expression tree is a representation of a certain code (expression) in a form of a binary tree, where each internal node is an operator, and each leaf represents an operand. Consider the given expression in a form of the expression tree:
((a+b)+c(d+e)+f)(g+h)
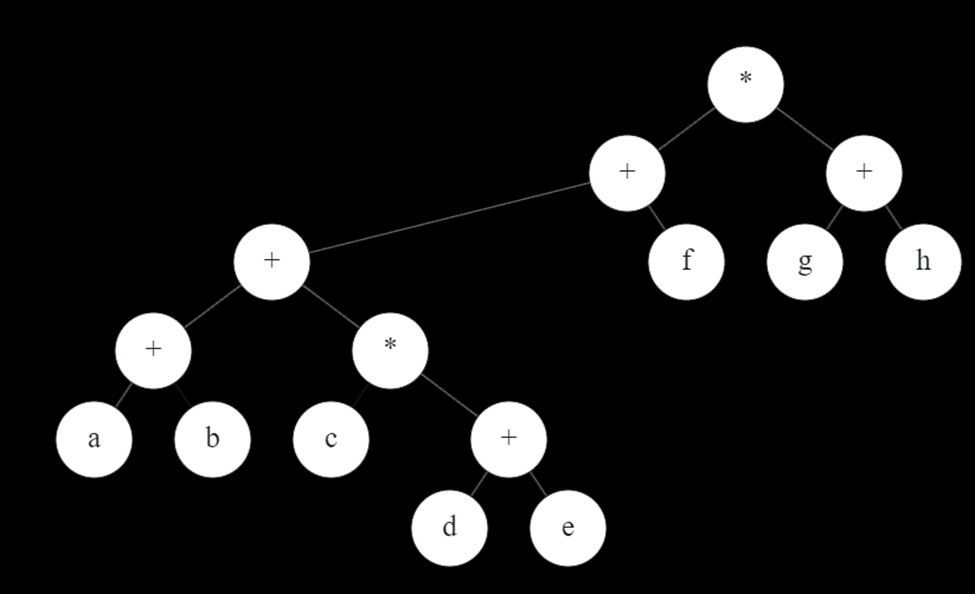
If the tree is traversed in preorder, then the result will be, we visit in the following order:
*+ + + a b *c + d e f + g h
For inorder:
a + b + c * d + e + f * g + h
For postorder:
a b + d e + c * + f + g h + *
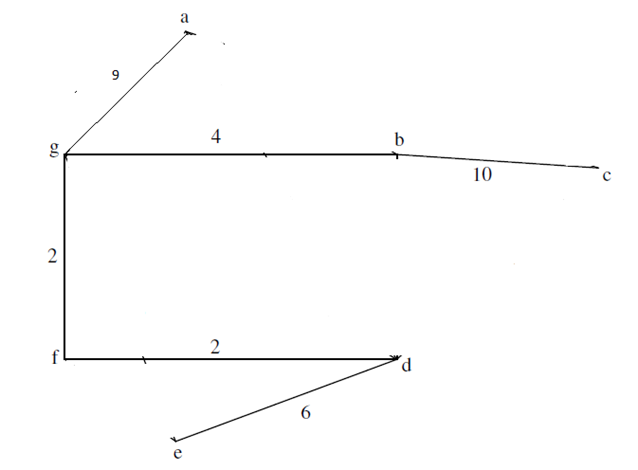
b) An MST of a graph is a subset of the edges of an undirected, edge-weighted, connected graph that connects all its vertices together, with the minimum possible total edge weight and without any cycles. We can run Prim’s algorithm on the given tree to find the MST.
Start with vertex B. The shortest edge from B is B-G – add it to the MST. Then, check for the edge with the minimum weight from all other edges. This is G-F, add it to the tree. Next, consider all the remaining edges, connecting this tree to the remaining vertices. This is F-D. Next, repeat the step – and this will be D-E. Next, the shortest edge is A-F. Finally, the remaining vertex is C, and the shortest edge is B-C. Now, all vertices are in the MST. The MST has the following form:
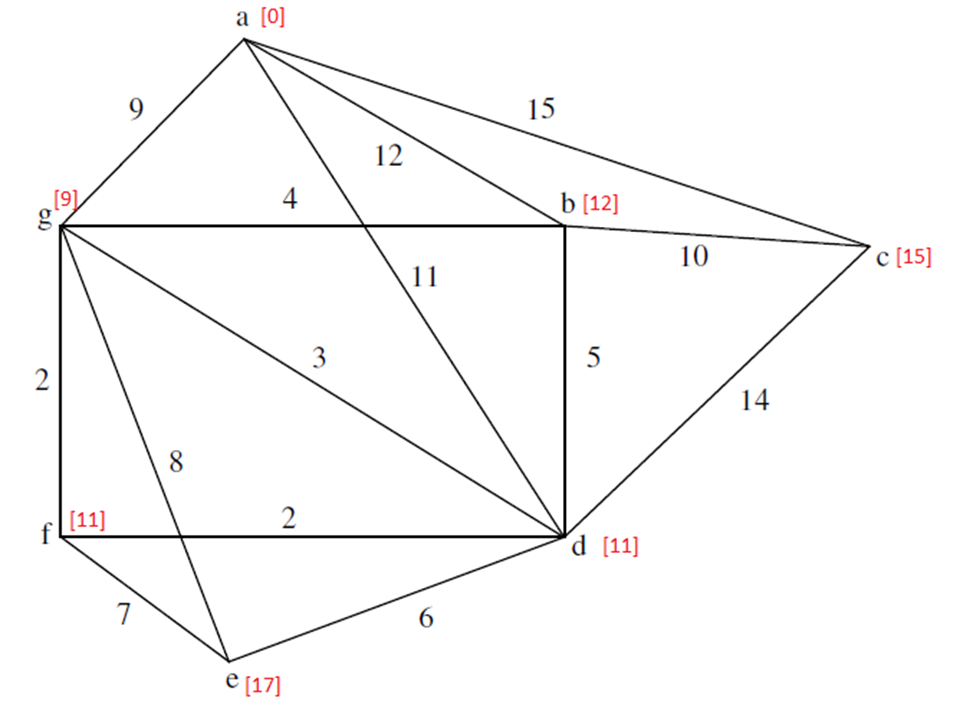
c) Select A, the distance to A is 0. The shortest distance to C is 15, the shortest to B is 12, to D is 11, and go G is 9. Select A-G. Through G, the shortest distance to B is 4, to D is 3, to E is 8, and to F is 2. Hence, the distance A-F is 9+2=11, A-B is 12, A-D is 11, A-E is 9+8=17. Next select A-D, from D, it is 14 to C, and so 11+14=25 in total, but A-C is 15, hence the distance from A to C is 15. Summing up, we get the following:
Question 2 (2nd of 3)
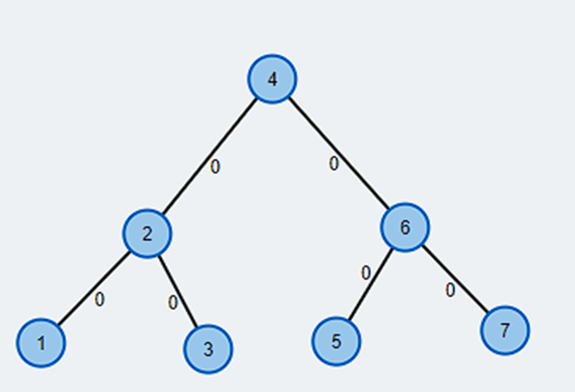
a) Such a tree will have the following form (disregard the zeros in the distances):
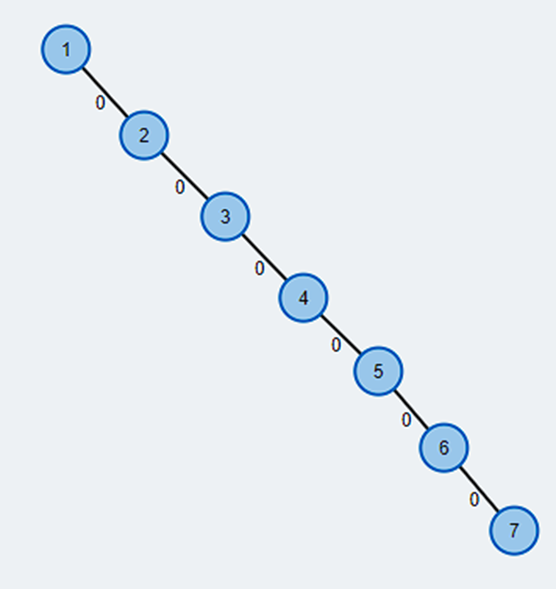
The problem with this tree is that this is a skewed tree. Therefore, the time of completion of a search algorithm will be O(n), which is large. This algorithm could be improved, for example, if taking the middle element as the root and divide it with half and make it like this:
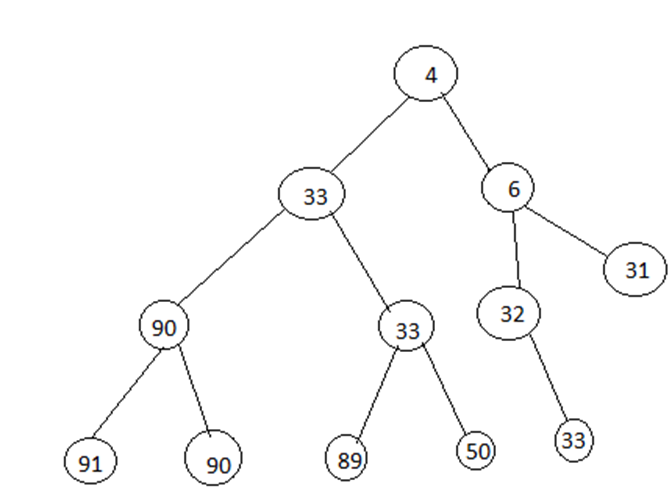
b) To be a min-heap, parent value should be less than both children values. Yes, A is a min-heap:
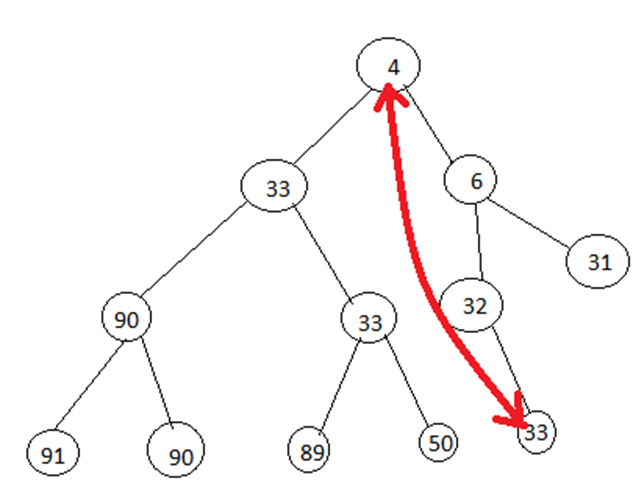
Now let’s delete the min value. Change it with 33 like this:
Apply min-heapify procedure:
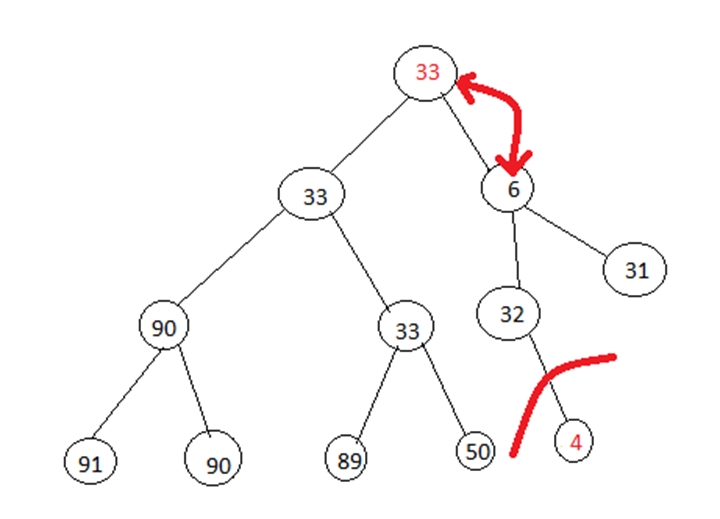
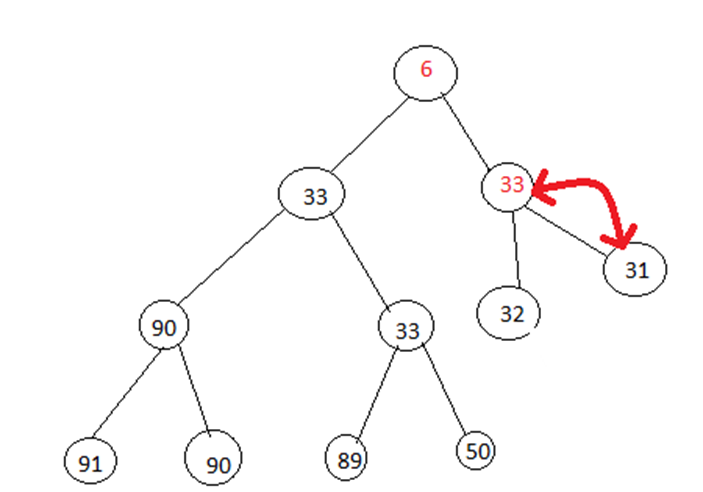
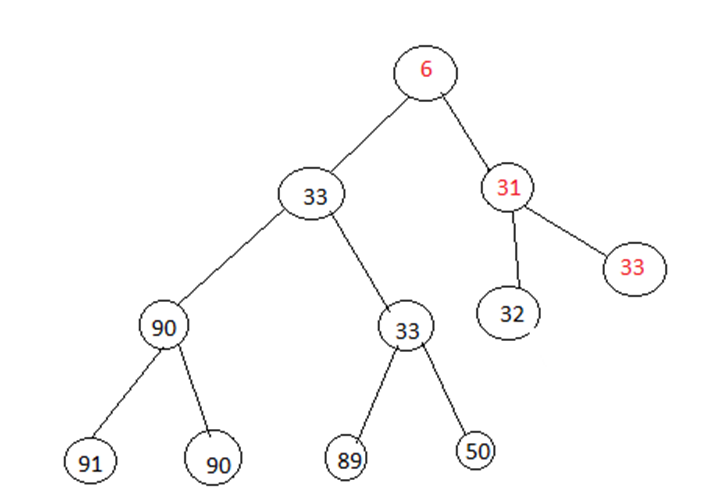
Now it is again min-heap.
c) The algorithm can be as follows:
- Insert at the bottom of the tree.
- Update the position of this element so that the min-heap property is satisfied.
- Check the sub-tree of its immediate parent.
- If the parent is greater than the element inserted, then swap the positions of parent and element.
- Keep swapping until we reach the root node.
Consider the example of the min-heap H:
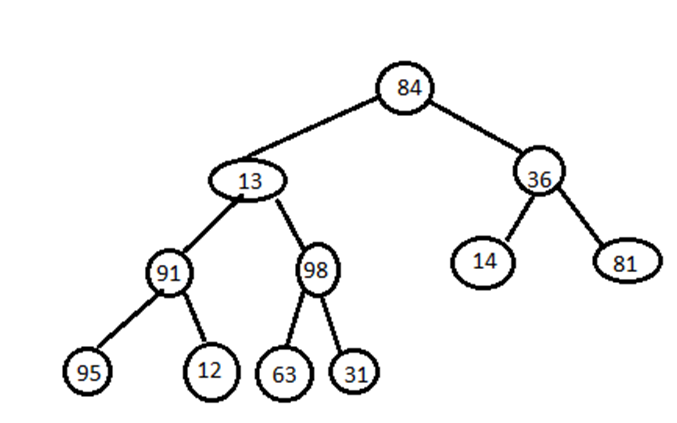
Re-arrange the heap to make it min-heap:
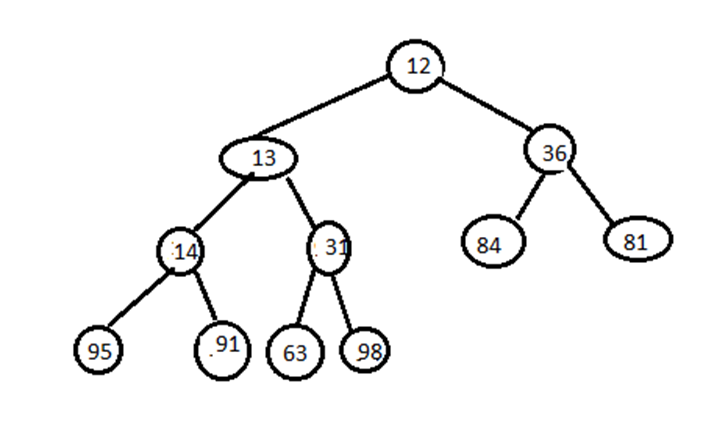
Now implement the algorithm. Insert 10 at the bottom of 81:
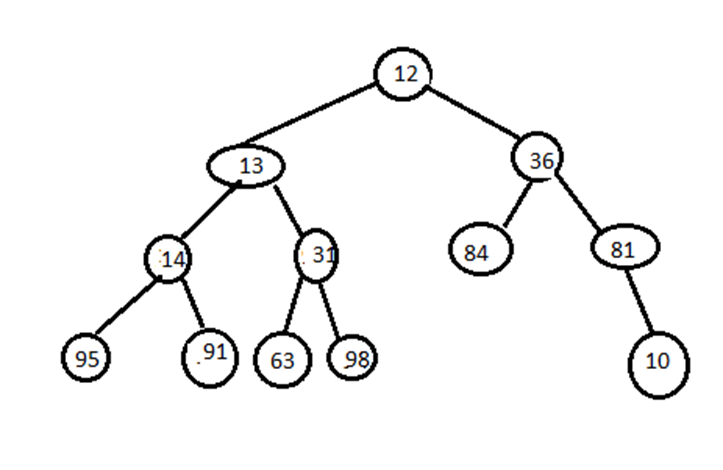
Now since parent is not less than this element, swap them. Next swap it with 36, next with 12:
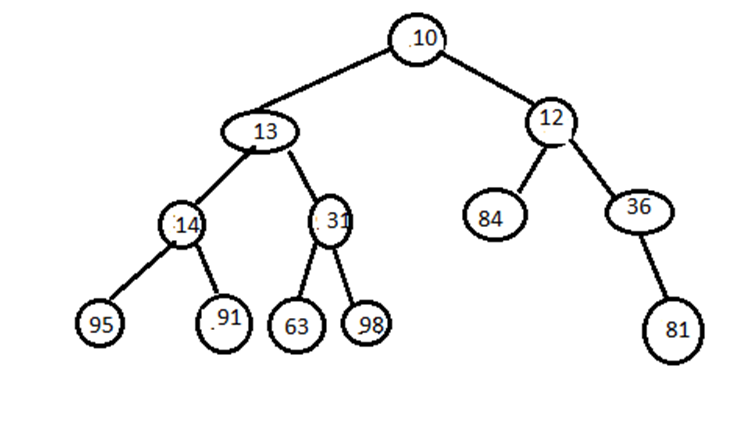
The result is again a min-heap.
Question 3 (3rd of 3)
a) Recursion is a way to define a problem in terms of itself. Recursive algorithms call themselves with input values to obtain the result for the current input by applying some basic operations. For example, expressions that are used in various sequences like arithmetic or geometric sequences may serve as an illustration of a recursive algorithm. The key components are:
- An algorithm should call itself, recursively.
- It should have a base case.
- It must change its state and move to the base case.
b) Consider an example of a recursive algorithm – computing factorials. The base case is that 1! = 1. Next, the algorithm itself can be expressed in Java is:
int fact(int n)
{
if(n == 1)
{
return 1;
}
else
{
return n * fact(n 1);
}
}By completing this algorithm in a cycle, we will always converge to the base case.
c) Creating a Stack class:
class StackClass
{
private int array[];
private int top;
private int cap;
//constructor
stackClass (int size)
{
array = new int[size];
cap = size;
top = -1;
}
// method that adds an element to the stack
public void push(int x)
{
if (isFull())
{
System.out.println("Stack oveflow");
System.exit(-1);
}
System.out.println("Adding " + x);
array[++top] = x;
}
// Method extracts the top element from the stack
public int pop()
{
if (isEmpty())
{
System.out.println("Stack underflow");
System.exit(-1);
}
System.out.println("Extracting " + peek());
// уменьшаем размер stack на 1 и (необязательно) возвращаем извлеченный элемент
return arr[top--];
}
// Method returns the top element of the stack
public int peek()
{
if (!isEmpty()) {
return array[top];
}
else {
System.exit(-1);
}
return -1;
}
// Method gets stack size
public int getSize() {
return top + 1;
}
// Method checks if the stack is empty
public boolean isEmpty() {
return top == -1; // or return getSize() == 0;
}
// Method checks if the stack is full or not
public boolean isFull() {
return top == cap - 1; // or return getSize() == cap;
}
}
Creating class for queue
class QueueClass {
private static int queue[];
private static int capacity, rear, front;
//constructor
QueueClass (int size) {
capacity = size;
front = rear = 0;
queue = new int[capacity];
}
// Method inserts an element to the queue
static void insert(int item) {
// checking if it is full
if (capacity == rear) {
System.out.printf("Queue overflow");
return;
}
else {
queue[rear] = item;
rear++;
}
return;
}
//method for deletion
static void delete() {
// checking if it is empty
if (front == rear) {
System.out.printf("Queue underflow");
return;
}
else {
for (int i = 0; i < rear - 1; i++) {
queue[i] = queue[i + 1];
}
if (rear < capacity)
queue[rear] = 0;
rear--;
}
return;
}